Observing linearisability
There is a good discussion by Dziuma et al with some more precise definitions on which I’m going to base this article.
The setup is a distributed system with some client processes which can perform operations (think: RPCs) on some remote data objects (think: a single-value register). The operations, being remote, take some nonzero amount of time between the client invoking the operation and being notified of its completion. The clients are themselves sequential and the RPCs are synchronous (i.e. blocking) so there is no funky interleaving of things within each client. Each data object also has a semantics which is well-defined at least for sequences of operations that do not overlap.
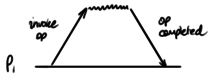
In order to get any sensible work done in such a system, we need some guarantees about the behaviour of the data objects on which we can rely. It would be pretty useless to allow concurrent operations to result in arbitrary behaviour, so we basically insist that each client sees each data object behaving as if the operations on it occur in some linear sequence. But beyond that, it seems that pretty much anything goes. Here’s a two-register program that is so-called slowly consistent:
x := 0 | x := 1
assert(x == 1) | assert (y == 1)
y := 1 | assert (x == 0) // WTF?
I’ve met this sort of nonsense before in systems that have weak memory models and they are not easy things to program correctly. On the other hand, they can be really efficient to implement as you can stick all sorts of caches in them to speed things up at the cost of making things appear to happen in different orders in different places.
Instead of this mess I want to look at the two strongest kinds of guarantee, known as sequential consistency and linearisability. A system is sequentially consistent if, roughly, there is a single global sequence of operations consistent with each client’s observations. For instance, this program is sequentially consistent:
x := 0 | y := 2 | assert (y == 2)
x := 1 | | assert (x == 0)
| | assert (x == 1)
This is because this sequence of operations is consistent with all clients:
x := 0 | |
| y := 2 |
| | assert (y == 2)
| | assert (x == 0)
x := 1 | |
| | assert (x == 1)
A sequentially consistent system is linearisable if additionally, roughly, the sequence of operations is consistent with the real-time order of events. More precisely, if an operation A completed strictly before operation B was invoked (in real-time) then linearisability insists that A occurs before B in the resulting sequence whereas sequential consistency imposes no such constraint.
At first sight this seems like a reasonable constraint, but there’s something philosophically shaky about it: if A and B occur at different places in the system, their order might not be well-defined. There is, fundamentally, no way to define a global linear “real” timeline in a distributed system, and whenever you see anything that relies on the existence of such an impossible thing you should be suspicious.
On the other hand, sequentially-consistent-but-not-linearisable systems are strange: you can see an operation complete strictly before another one begins and yet it is legitimate for the system to behave as if they ran in the other order. Linearisability certainly seems like a more useful constraint when it comes to programming in a distributed system.
From one viewpoint, linearisation-checkers like Aphyr’s Knossos do impose a global ordering on the events in the system and use this to detect linearisation failures. But from another viewpoint, Knossos is also running within the system, which raises the question of whether its notion of “real” time is valid. Could Knossos decide on a sufficiently bad timeline that it incorrectly detects a linearisation failure?
The answer is a somewhat anticlimactic “no”, for the following reasons. When using Knossos, each client logs the invocations and completions of its operations into a single linear log.
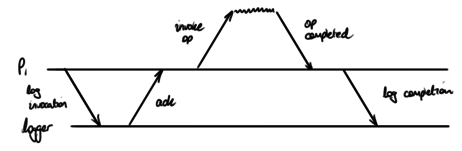
Notice that this logging is conservative: the invocation is logged (and acknowledged) before the operation is invoked, whereas its completion is logged after it completes.
Now consider a pair of operations such that the first is logged as having completed before the second starts. In this situation these events must occur in the following order:
- Operation A completes
- Completion log message sent (because logging occurs after completion)
- Completion log message received (because the network is causal)
- Message received logging the invocation of operation B (because it was logged after the completion of A)
- Acknowledgement of B’s invocation sent (because the logger is causal)
- Acknowledgement of B’s invocation received (because the network is causal)
- Operation B invoked (because invocation occurs after logging is acknowledged)
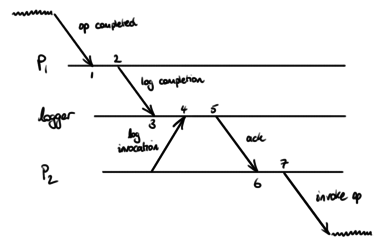
Therefore if the log shows A completing before B is invoked then A must genuinely have completed before B was invoked. The converse is, of course, false: the log may not contain all complete-before-invoke pairs, at least partly because such a set is ill-defined. But Knossos is only checking for partial correctness by design anyway, so it does not really matter if some of these pairs are missing.
In a sense, therefore, Knossos is checking for sequential consistency of the system under test together with the Knossos log itself. If this larger system is not sequentially consistent then nor is it linearisable, and therefore the system under test is not linearisable either.
This also explains why sequential-consistency is more useful than it looks: if you can observe two nonoverlapping events occurring in one sequence but the system behaves as if they occurred the other way round, then the system together with you, the observer, is not sequentially consistent and therefore not linearisable.
I wonder whether some kind of converse is true: if you have a system that has some nonlinearisable behaviour, is it the case that you can connect its clients together in a way that violates sequential consistency? In other words, is the technique used by Knossos complete?