Pre-voting in distributed consensus
Ongaro’s thesis
describes an optional PreVote phase in Raft that is designed to prevent a
partitioned server from disrupting the cluster by forcing a re-election when it
rejoins the cluster. This article is about the benefits of using a similar
mechanism in a Paxos implementation.
The trick with showing the liveness of a Paxos cluster boils down to making
sure that nodes send the right quantitiy of prepare (a.k.a. phase 1a)
messages: too few can lead to deadlock, whereas too many can lead to livelock.
The other messages (promised, proposed and accepted) affect the safety of
the system, but prepare messages have no bearing on safety. In contrast, as
long as they are sent in a timely fashion the other messages have no real
bearing on liveness.
Presentations of Paxos often show its liveness property by assuming the existence of a distinguished leader which is elected by some unspecified external process. Raft has no need for a separate leader-election process as it has a built-in system of timeouts instead, which is much cuter. Ongaro’s thesis does not show that Raft satisfies any particular liveness properties, but it certainly seems plausible that it works. [I am unaware of much further literature on Raft’s liveness properties but please get in touch if you know of some.]
It’s possible to run Paxos without an external leader-election process in much
the same way that Raft works, and I found that a similar PreVote phase was
very helpful in ensuring its liveness. The mechanism is as follows. Each term
number has a well-defined owner, and nodes consider the owner of the term of
the most-recently-chosen value to be the leader, as long as this value was
chosen sufficiently recently. In more detail, each node is in one of four
states:
-
Leader - this node owns the term of the most-recently-chosen value that it knows about, and this value was chosen very recently.
-
Incumbent - this node owns the term of the most-recently-chosen value that it knows about, and this value was chosen recently, and not very recently.
-
Follower - some other node owns the term of the most-recently-chosen value that it knows about, and this value was chosen recently or very recently.
-
Candidate - no value is known to have been chosen recently.
The definitions of recently and very recently are in terms of timeouts set by the system’s operator. More formally, nodes implement the following state machine.
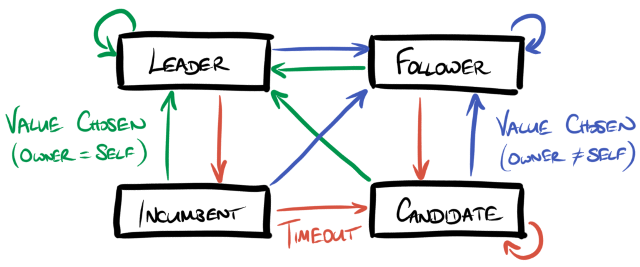
State transitions due to timeouts are shown in red, and those due to values being chosen are shown in green (if in a term owned by the current node) or blue (if in a term owned by another node). If a leader times out and becomes an incumbent it also attempts to propose a new no-op value in a term that it owns which if successfully chosen will reinstate it as a leader again. The timeouts should be set such that leaders become incumbents in good time to become leaders again before any followers become candidates. Note that each timeout is implemented based on the node’s local clock and there is no need to share time values between nodes, so there is no need for any kind of clock synchronisation in this setup.
It is hopefully reasonably obvious from this that eventually either there exists a node that has learned the next value or else all nodes have become candidates.
When a candidate times out it remains a candidate but also attempts to make
progress (i.e. to learn that a later value is chosen) as follows. Firstly, it
broadcasts a seek-votes message indicating the latest value it learned. The
recipients of this message may do one of three things:
- If the recipient knows that a later value has been chosen then it responds
with an
offer-catch-upmessage indicating as such. - If not, but the recipient believes there is an active leader (i.e. they are not themselves a candidate) then the message is ignored.
- If neither of the previous cases apply then the recipient responds with an
offer-votemessage indicating the greatest term number for which it has previously sent apromisedmessage.
If a candidate receives an offer-catch-up message it communicates directly
with the sender in order to learn the missing values. If instead it receives
offer-vote messages from a quorum of its peers then it sends out a prepare
message using a term that is no less than any of the terms received in the
offer-vote messages, and runs the usual protocol from there on.
Addendum 2020-05-24: simbo1905
notes
that some variants of Paxos allow the quorums to differ between
the phases of Paxos and/or allow the configuration of the cluster can be
changed dynamically, and in such variants we need to be more precise about
exactly which quorum we mean when collecting offer-vote messages. The node is
trying to choose a value for the first unchosen instance, which requires it to
run both phases of the protocol, so in fact it should wait for offer-vote
messages from both a phase-I quorum and a phase-II quorum in the
configuration that corresponds with the first unchosen instance. If it cannot
contact a quorum for both phases then there is little point in proceeding since
it will not be able to make meaningful progress.
Quiescence
The protocol as described is eventually quiescent: absent any external stimulation (timeouts or client activity) eventually the system reaches a state where there are no messages either in flight or being processed. This is, approximately, because there are no loops in the graph of the messages that can be transmitted on receipt of each type of message:
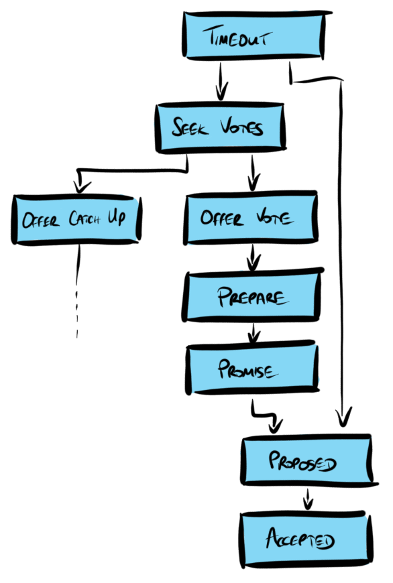
This helps to completely rule out certain kinds of livelock. The situation is a
little more complicated than this because a cluster reconfiguration requires a
new phase 1 to take place, so an accepted message can result in a prepare
message too, but this doesn’t result in livelock as there can only be finitely
many pending reconfigurations.
If the round-trip time between nodes is bounded then this observation puts a bound on the time it takes for the system to become quiescent after external stimulation. In particular if there are no pending proposals at any node then it takes at most three round-trips to become quiescent.
Liveness
As noted above, eventually either there exists a node that has learned the next value or else all nodes have become candidates. It remains to show that if all nodes are candidates, at least one of which can communicate with a quorum of its peers, then the system still makes progress.
If candidates wake up too frequently then the system will never become quiescent, but if they wake up too infrequently then the system will take a long time to recover from an unexpected failure of the leader. Absent a tight bound on the network’s round-trip time, it is preferable that candidates wake up with random and growing timeouts because as long as the timeouts grow to be sufficiently long compared with the communication round-trip-time between nodes, eventually-almost-certainly one candidate will time out at a point in time when the system is quiescent and no other node will time out for at least three round-trips.
Sketch Theorem Such a candidate, if connected to a quorum of peers, makes progress.
Sketch Proof. Let n such a candidate. As noted above, its peers are
eventually either all candidates or else contain a node which has learned some
later values. Also, eventually-almost-certainly, it is the only active node. It
broadcasts its seek-votes message and receives responses from its peers. It
is connected to a quorum of peers, so it either receives an offer-catch-up
message or a quorum of offer-vote messages.
In the former case it learns some later chosen values from the sender. In the
latter case it sends out a prepare message to start phase 1 of the usual
Paxos algorithm. Since n is the only active node, no other prepare message
has been sent since any of its peers sent out their offer-vote messages,
which means that they will all respond with promised messages.
On receipt of this quorum of promised messages, n may propose a value. If
none of its peers have previously accepted a value in an earlier term then it
may freely choose to propose any value. Typically it would choose a no-op
action in this situation.
On the other hand if some of its peers have previously accepted a value then it
must propose one of their values according to the rules of the Paxos algorithm.
Again since n is the only active node then no other promised messages will
have been sent before its peers receive the proposed message, so the proposal
will result in a quorum of accepted messages which results in the proposed
value being chosen and learned as required. QED.
Unboundedly large messages
The time it takes to send and receive a message is a function of its size, so
it is only safe to assume that the round-trip time is bounded if messages have
bounded size. In practice if a message is too large then nodes time-out before
it is fully delivered, which can lead to a leadership election, and also breaks
the liveness proof above: if promised messages may take arbitrarily long to
deliver then there may never be a time when there is a unique active node and
therefore no election may ever succeed. It’s a good idea to limit the size of
values and to set any timeout limits accordingly.
Alternatively, one could split up promised and proposed messages into
chunks of bounded size and reset the timeout timer each time a chunk is
received.
Abdication
There is no need for nodes to send out prepare messages for terms that they
own, and this can be used to implement an abdication mechanism allowing the
current leader to step down having determined its successor. The alternative to
abdication is for the leader to simply stop sending out any messages and to
wait for the other nodes to time out. The disadvantages of this include
-
the system is effectively unavailable until the timeouts expire, whereas with abdication the new leader normally takes over within a few round-trips without any risk of contention
-
the new leader is chosen by a nondeterministic race, whereas with abdication the new leader can be selected explicitly. For example, if there are a number of clusters running in a shared environment then it may make sense to try and distribute the leaders as evenly as possible across the environment.
A leader abdicates simply by sending a prepare message for a term owned by
the new leader that is larger than the current term. Nodes should respond with
a promised message sent to the owner of the term and not to the original
sender, and from there the usual Paxos message flow leads to the new leader
owning the term of the next value to be chosen and therefore being recognised
as the cluster leader.
Alternatives
As mentioned above, there could be a completely separate leader-election
process which determines which node is permitted to send prepare messages.
This seems inelegant compared with the idea of building leader-election into
the consensus system, but could be appropriate if there are particular
requirements on how nodes may become leader that are not well-served by the
mechanism above.
Another strategy that implementations sometimes use is to consider the leader
to have failed if a value has not been chosen for a period, and to immediately
send out a prepare message after this timeout expires. Raft (without its
PreVote phase) uses this kind of strategy. The main challenge with this
approach seems to be the selection of an appropriate term to put in the
prepare message: it’s common to choose a term that is slightly higher than
the greatest term seen so far in any known message. In practice this seems to
work ok although it does seem to suffer from (temporary) livelocks more. In
theory it’s a bit problematic: my attempted proofs that this works always
seemed to get stuck on the fact that there’s no guarantee that the selected
term is large enough, so any particular node may fail to be elected when it
times out. It’s not at all obvious that always there is eventually a node that
selects a high-enough term.
It was these failed proofs that led me to the idea of the seek-votes message
and offer-vote responses to determine an appropriate term for the subsequent
prepare message. With that idea, the proof fell into place.
Disruption on reconnection
As in Raft, this extra phase prevents nodes from triggering a new leader
election when they reconnect: out-of-date nodes receive a offer-catch-up
message before they have received a quorum of offer-vote messages. This means
that the leader tends to be stable for as long as it remains connected to a
quorum of its peers, and other nodes may only send a prepare message once
there is a quorum of nodes that believe the leader to have failed.
After a reconnection the system can get itself into a subtle and rare state in
which it’s still making progress, but some minority of nodes have entered a
later term than the one in which the majority is working. This means that this
minority can’t accept any proposals from the leader, but nor can they gather
enough offer-vote messages to trigger a leader election in a later term.
Instead, they continually receive offer-catch-up messages and learn new
values through the catch-up process. This may not be too much of a problem, and
the situation will resolve itself at the next election, but elections should be
relatively uncommon so the situation could last for many days. It’s also
operationally irritating: if it weren’t for this state then you could consider
candidate nodes to be indicative of problems in the cluster for monitoring
purposes.
The fix is to include the candidate’s current term in its seek-votes message,
and if a leader receives a seek-votes message containing a later term then it
performs another phase 1 at an even later term. This has the effect of keeping
a stable leader while allowing the other nodes to start accepting its proposals
again, which avoids upsetting the monitoring system.
Addendum 2017-08-31
There’s an enthusiastic review of this article over on simbo1905’s blog which gives some more intuitive coverage of the ideas in this article as well as some thoughts on how this mechanism relates to the one in TRex.
Addendum 2020-12-15
By “Raft” in this post I mean the full protocol including the PreVote and
CheckQuorum features. It doesn’t work without
them,
so it’s a bit misleading to describe them as “extensions” or “optimisations”.
At least one major implementation of Raft gets this wrong
today
and is buggy by
default,
with predictably disastrous
consequences.