Timezone-sensitive rounding
Here’s an example of the sort of thing you can do with local-universal time
diagrams. Suppose you have
some data about events that occurred at particular times in a system, such as
log messages. You want to calculate some aggregate statistics about its
behaviour over time. For instance you might want to aggregate all the events
from 00:00 to 03:00 together, and then all the events from 03:00 until
06:00, and so on for every 3-hour window in the day.
The tricky bit is that you want to do this in local time, so when the clocks change for daylight savings time you want some windows to be shorter or longer than normal so that the times continue to line up with the local times that are a multiple of 3 hours past midnight.
Because the data contains machine-generated timestamps and is all about events
that have occurred in the past, you can store the actual event times in
UTC. The
question is then how to identify the window in which any given data point lies.
A good way to do this is to truncate each time, rounding it down to the nearest
multiple of 03:00, and then use this truncated time to identify events that
occur in the same window.
On a local-universal time graph the equally-spaced local times can be marked on the vertical axis:
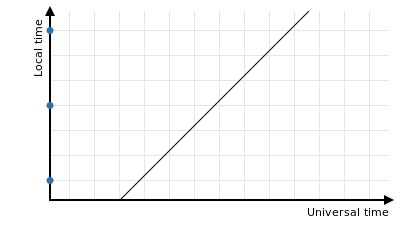
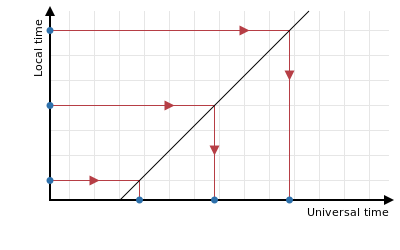
Of course if the clocks are not changing then this means that the “rounded” times are also equally spaced on the horizontal axis, although they might not be nice round times if the timezone’s offset from UTC is not a multiple of 3 hours:
The basic idea for truncating a time is to convert it to local time, round it down, and then convert it back to universal time again:
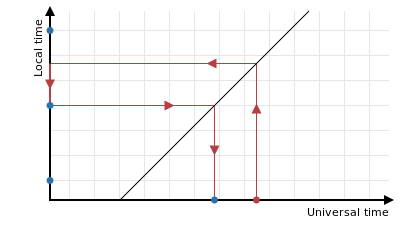
Of course, with time calculations nothing is ever so simple.
When the clocks go back
When rounding down a time just before the clocks go back, this process still works correctly:
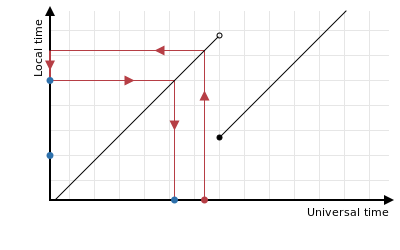
The process might also work correctly when rounding down a time just after the clocks go back:
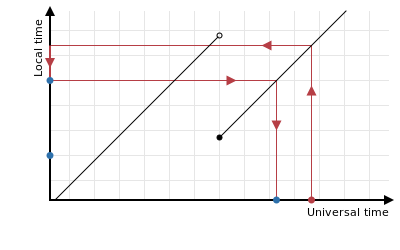
Of course you have to be careful with the “convert back to universal time” step, because in both of the cases above there are two universal times corresponding with the rounded local time. Fortunately it’s not too hard to compute them both and choose the right one.
There are other cases just after a clock change where the process doesn’t work. Rounding the local time down would give a result that’s too early. Instead it looks like you have to round the local time up:
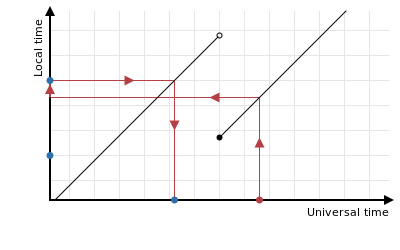
Notice that this is nothing to do with the ambiguity in the “convert back to universal time” step, because if we had rounded the local time down here then there would have been no ambiguity.
Futhermore it’s not enough to try both rounding up and down, because sometimes you might even need to skip a rounded local time when rounding it up:
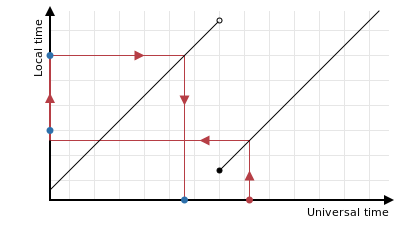
The problem in these cases is really that the input time and the result are on opposite sides of the time when the clocks change. We’re looking for the greatest possible rounded time, but the naive process might yield a time that’s far too early. The error is bounded by the amount by which the clocks have changed. Fortunately there’s no need to do any kind of expensive search for a better time to correct for this, because we know that there’s no “rounded” universal time in between the input time and the transition (inclusive) and this means that it’s sufficient to go back to just before the transition and try and round that down instead:
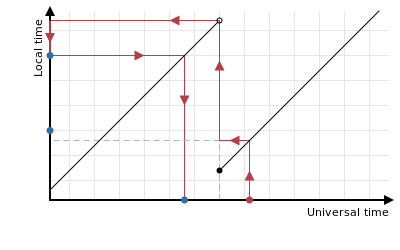
Another problem that can arise when the clocks go back is that sometimes you do not want to duplicate a rounded time. For instance, it’s common for windows to be some number of days long, so that typically each window will start at midnight. However if the clocks are set back across midnight then some days will contain two midnights and yet you might not want to consider the second such midnight to be “rounded”:
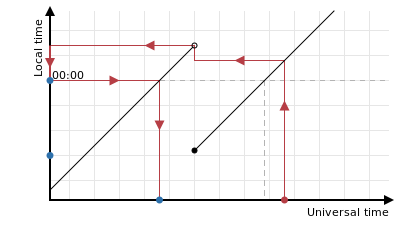
There’s no technical reason for choosing one way or another: it’s purely a business decision as to which duplicated times should be considered to be rounded. Sometimes it’s ok to use both, but in other situations you might want only the earlier or the later of the two.
When the clocks go forwards
When the clocks are set forwards there are some local times with no corresponding universal time, which raises the question of what one should do if a rounded local time falls in this gap:
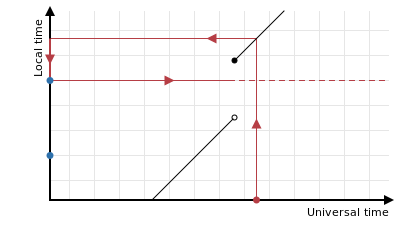
The solution depends on whether or not you want to consider a transition time to be rounded if it contains a rounded local time. If you do want to do this then the transition time is the correct result:
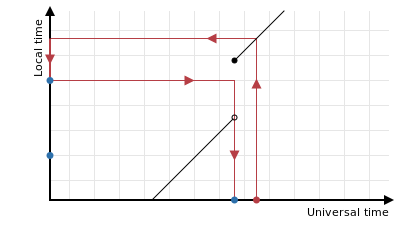
However if you do not want to consider the transition time to be rounded then you know that there’s no other rounded time in between the input time and the transition (inclusive) which means that it’s sufficient to go back to just before the transition and try and round that down instead:
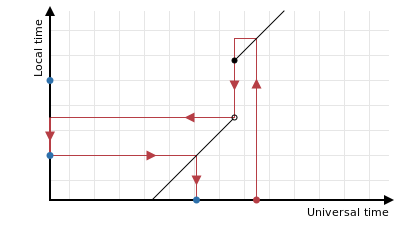
As above, there’s no technical reason for choosing one way or another: it’s purely down to your requirements.
Conclusion
Rounding a time is a little tricky when you need to work in local time and account for clock changes. A local-universal time diagram helps to visualise some of the problems you might face, to identify some of the decisions you need to make, and to design a robust solution.