UPaxos and primary-backup replication

This is a riff on Vertical Paxos and Primary-Backup Replication by Lamport, Malkhi and Zhou, showing how primary-backup replication can be seen as a special case of UPaxos. Vertical Paxos uses an external master system to manage the cluster’s configuration, but the same technique also supports modelling a redundant set of master nodes as a first-class part of the cluster as shown here. The quorums used are more intricate than the simple majorities usually used in consensus implementations, and in particular the quorums used for the two phases of the algorithm are distinct. I think Lampson observed this possibility; it’s used in Vertical Paxos and it is fundamental to Howard, Malkhi and Spiegelman’s FPaxos and UPaxos too.

The advantage of modelling primary-backup replication in this way is that the correctness properties of Paxos carry across, giving clear justifications for the safety and liveness of the system.

Primary-backup replication

A primary-backup replication system has a set of data nodes, comprising a single distinguished primary and some number of backups, that work together to accept data from clients in a way that ensures no data is lost even if some of the nodes fail. The clients write data to the primary which then forwards it on to the backups. The primary requires a successful response from all backups before acknowledging a write to a client.

The trouble with requiring all backups to acknowledge all writes is that sometimes one of the backups may fail, which brings the entire system to a halt. The solution is to have a separate master process that springs into action on failure of a backup and alters the cluster’s configuration to remove the need for acknowledgements from the faulty backup. The master may also alter the cluster’s configuration for other reasons, such as

• to select a different node as the primary,

• to add new backup nodes to increase the level of redundancy in the system, or

• to remove nodes from the backup set while planned maintenance is in progress.

The master process itself is usually implemented as a redundantly-distributed system, often a replicated state machine, to reduce its risk of failure, since a failure of the master may lead to a full-system outage.

UPaxos

UPaxos is an extension of Paxos that supports reconfiguration without limiting the length of the pipeline of in-flight requests, and which can perform some reconfigurations without a pipeline stall. Its correctness is assured by preserving a list of invariants, shown in figure 2 of the UPaxos paper. The important one for this discussion is invariant P1 which says that in each era e there are sets of quorums (sets of nodes) Q^I_e and Q^II_e which are known respectively as the phase-I quorums and the phase-II quorums, and which are such that every phase-I quorum in era e must intersect every phase-II quorum in era e and also every phase-II quorum in era e+1.

Quorum design

In many distributed consensus implementations, quorums for both phases are defined as the majority or weighted-majority subsets of some set of nodes, but there are many other possibilities and primary-backup replication in particular can be modelled by the following quorum design.

The system has some number of master nodes (M) and data nodes, of which one is usually nominated as a primary (P) and all others are backups (B):

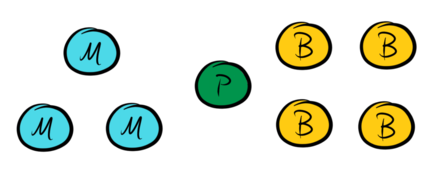
A Paxos-based system is normally in phase-II for an extended period of time, and the phase-II quorum is used to accept client requests. A primary-backup system accepts client requests at the primary, replicates them to all backups, and then responds to the client without any involvement from the master nodes. Therefore the set of data nodes forms a phase-II quorum:

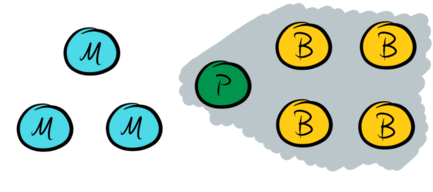
However, the set of data nodes cannot be the only phase-II quorum because the failure of a single data node would result in no further progress being made. To prevent this, say that any majority of the master nodes is also a phase-II quorum, which effectively allows the master nodes to coordinate progress in the system in the event that a data node fails:

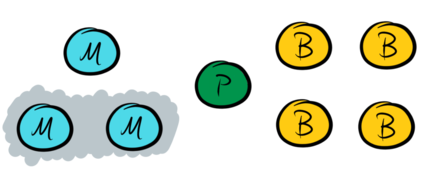
Recall that the UPaxos invariant requires that each phase-I quorum intersects each phase-II quorum in the same era. Therefore the phase-I quorums must comprise at least a majority of the master nodes together with any single data node:

With this design, all phase-I quorums intersect all phase-II quorums as needed to ensure the algorithm’s correctness.

The way that the quorum structures on the master nodes and the data nodes are combined here seems to be quite general. Ignoring reconfiguration, say that a two-phase quorum structure is a pair of sets of sets of nodes ⟨Q^I, Q^II⟩ such that every q^I ∈ Q^I intersects every q^II ∈ Q^II. Given any weight function w on nodes with total weight W = ∑_n w(n), and any positive integer thresholds t^I, t^II having W < t^I + t^II, the pair ⟨ {q. t^I ≤ ∑_{n ∈ q} w(n)}, {q. t^II ≤ ∑_{n ∈ q} w(n)} ⟩ is a two-phase quorum structure. Also, for any pair of two-phase quorum structures ⟨Q^I, Q^II⟩ and ⟨R^I, R^II⟩ the pair ⟨{q ∪ r. q ∈ Q^I, r ∈ R^I}, Q^II ∪ R^II⟩ is also a two-phase quorum structure. I’m not sure that this generality is all that important, but thought it worth saying anyway.

Liveness and failover

Data-node-led failover

To ensure liveness, it is possible to use the pre-voting mechanism described earlier with some fairly small modifications to the mechanism and associated correctness proof.

The primary node usually behaves as the leader with the masters and backups behaving as its followers. The data nodes all learn values for increasing slots at some minimum frequency; if there is not enough client activity to reach this minimum frequency then the leader times out, becomes an incumbent, and proposes a no-op value as a keepalive. If no value is learned for long enough, data nodes may time-out, become candidates, and attempt to take over as leader by broadcasting a seek-votes message. Because they seek a phase-I quorum of votes, this message need only be broadcast to the master nodes.

The master nodes need only act as acceptors and not propose or learn any values. They typically act as followers of the primary and become candidates if they believe it to have failed, perhaps using a timeout to detect missing heartbeats or some other failure detection mechanism. As candidates they lack ambition and simply wait for one of the data nodes to attempt to become leader after a failure: they need not timeout and seek votes as normal candidates do. Master nodes may send an offer-vote message in response to a seek-votes messsage if they are candidates. There is little point in master nodes sending offer-catch-up messages as they learn no values and hold no data. It is interesting to notice that the master nodes are almost completely passive and need not elect a leader or even communicate with one another to ensure the safety and liveness of this protocol.

If one of the data nodes fails then the primary will stop being able to accept client requests. Eventually the data nodes start to become candidates and broadcast seek-votes messages to the master nodes. Eventually, also, the master nodes become candidates and respond with offer-vote messages. On receipt of a quorum of offer-vote messages a node may send a prepare message to the master nodes, which respond with promised messages, and on receipt of a quorum of these the node has completed phase-I and may start to propose some values.

Recall that the phase-II quorums are the set of all data nodes, or else the majority subsets of the master nodes. One of the data nodes has failed, so the former quorum is not available, and therefore the active node must use a majority of the master nodes to accept its proposals. If there are any pending values, represented by promised messages containing previously-accepted values, then the Paxos invariants dictate that it must propose these first. Any gaps can simply be filled in with no-op values.

Having learned all pending values, it remains for the active node to reconfigure the system so as not to require the failed data nodes for progress any more. Reconfigurations are actions in the replicated state machine, so the active node proposes a suitable reconfiguration to the masters and on receipt of a quorum of acceptances it may start to accept client requests again without further involvement from the masters, which restores the system to its usual pattern of running.

This describes the happy path through the failover process, with a single well-connected active data node and no other in-flight messages. The failover process may not always successfully restore the system to normal running while there are multiple active nodes sending concurrent, clashing messages, but it is possible to avoid this situation, eventually-almost-certainly, with suitable timeouts because the protocol is eventually quiescent.

This means that the system satisfies a liveness property that is approximately the following.

If a data node can eventually

• contact a majority of master nodes,

• determine a suitable configuration of the system for further work, and

• wake up at a time when there are no in-flight messages, and no other node is active or becomes active before all this node’s messages are processed,

then the system eventually makes progress.

The first two antecedents are satisfied if enough nodes are functioning correctly and the network is not too badly partitioned, and the third can be satisfied eventually-almost-certainly by using random, growing, timeouts at each data node.

The speed of this failover process is largely determined by the time between a node failure and a quorum of master nodes becoming candidates due to missed heartbeats, assuming that the new configuration can be selected and activated immediately. The time between heartbeats is essentially a tradeoff between failover latency and load on the master nodes, but could reasonably be as short as tens-to-hundreds of milliseconds for small clusters that need high performance and may be as long as a handful of seconds in larger or calmer clusters.

Master-node-led failover

It is also perfectly possible for one of the master nodes themselves to lead the failover process: it is elected as the cluster leader on a timeout, arranges for any pending values to be committed, then selects the new configuration and finally abdicates its leadership to the new primary.

This seems slightly more complicated to correctly implement, compared with having a data node lead the process, and its liveness property seems a little harder to state accurately too. It also puts extra load on the master nodes, particularly where there are a large number of failing-over clusters that share the same set of master nodes.

In contrast, an advantage of the masters taking a more active role is that in a multi-cluster setup it may make it easier to implement more complex cross-cluster policies about the distribution of data and primaries amongst the available nodes. This is also possible in the data-node-led failover described above, but requires more distributed coordination than if the masters select the new primaries directly.

It is likely that each particular implementation will be able to find a suitable balance of responsibilities between the data nodes and master nodes to trade off the respective advantages and disadvantages described here.

Choosing a new configuration

There are many options for how to decide on the new configuration, depending on the needs of the system operator.

The simplest approach is to do nothing automatically and require the operator to explicitly choose the new configuration, but this is unlikely to be satisfactory when operating at scale. That said, it is always an option to await operator intervention if an automatic strategy cannot find a viable configuration.

A simple automatic approach is to remove any purportedly-failed nodes from the cluster and continue, which ensures good availability at the risk that any subsequent data written to the cluster is not well-replicated and may subsequently be lost. This can be improved by only removing nodes as long as some minimum level of replication is not breached, and awaiting operator intervention if there is no way to do so.

A more robust alternative would be to select a set of replacements for the failed nodes and configure the system to use them instead. It may take some time to bring the replacement nodes in sync with the rest of the cluster, during which period the system may be unavailable or may be allowed to run with reduced resilience. In practical situations it’s likely that the topology of the underlying infrastructure has to be taken into account for this.

Proposals to master nodes

It may not be wise to propose client values directly to the master nodes, because master nodes are frequently shared between a large number of clusters and even a brief network partition affecting many clusters may result in the masters being overwhelmed by proposals. As long as the values are sufficiently well-replicated, it is possible to arrange for the masters to accept proposals that simply point to the values stored elsewhere without affecting the safety or liveness of the system.

The actual mechanism for doing this depends heavily on the implementation details of the system, which is another way of saying that I frankly haven’t thought about it in great detail at this point. The two Vertical Paxos algorithms describe some fairly abstract possibilities, and UPaxos section III.A has a very high-level description of how the necessary invariants can be preserved without needing all participating nodes to receive and process client values.

A subtle and vital feature is that promised messages from master nodes indicate correctly whether or not they have previously accepted any values. If this information is missing then the effects are quite insidious: even if it is missing the system will recover correctly from reasonably clean network partitions, because master nodes do not accept any values in normal running. However if, for example, a partition were to occur and heal but during the recovery process a second partition were to occur then there is a significant risk that the cluster state could diverge.

Mathematical details

The system’s e^th configuration C_e comprises:

• a non-negative integer weight w_e(m) for each master node m,
• a set D_e of data nodes, and
• a distinguished primary data node p ∈ D_e

Given these data, define:

• M(w_e) to be the set of all master quorums: sets of master nodes containing strictly more than half of the total weight,
• Q^I_e = { {d} ∪ m. d ∈ D_e, m ∈ M(w_e) }.
• Q^II_e = {D_e} ∪ M(w_e).

It is straightforward to see that every q^I ∈ Q^I_e intersects every q^II ∈ Q^II_e.

There are two kinds of stall-free reconfigurations that can be performed with this setup:

• adding a collection of data nodes to D_e (but not removing any nodes), and

• changing the weight of at most one master node by at most one unit.

This is because if the change from configuration C_e to C_e+1 is of one of these two types, then every q^I ∈ Q^I_e intersects every q^II ∈ Q^II_e+1, and because the primary node p has a casting vote between these two configurations.

More general (i.e. arbitrary) reconfigurations can also be performed using the era-skipping mechanism of UPaxos to skip over an era containing no quorums, with the associated possibility of a pipeline stall.

Generalisations

Primary-backup replication requires all data nodes to accept a value before considering it committed, but UPaxos supports many more options. For instance, if all-but-one data node were required to accept each value then the failure of a single data node would not require a disruputive reconfiguration in order to make further progress. To support this mode of operation without breaking any invariants, each phase-I quorum would need to comprise a majority of the master nodes together with a pair of data nodes.

More generally, the primary could require acceptances only from a majority of data nodes before a write is committed. In this case, each phase-I quorum would need to comprise a majority of the master nodes together with a majority of data nodes.

In fact, if there are B backup nodes then for all b ≤ B the system can be configured to usually require acknowledgements from the primary and just b of the backups in phase II by requiring 1+B-b of the data nodes in each phase-I quorum. The two main reasons for adding nodes to a primary-backup system are to increase redundancy and thereby increase the system’s fault-tolerance, and to add more capacity to handle a greater amount of read traffic. Reducing the number of acknowledgements required to accept a write clearly reduces the system’s resilience, but where capacity is the limiting factor on the number of nodes the ability to fine-tune the system’s fault-tolerance is valuable. Extra care is needed if b ≤ B/2 because in this situation it is possible to be able to continue to commit data (i.e. make progress in phase II) despite the failure of so many nodes that further leader elections (i.e phase I) cannot complete, which is a tricky-to-spot latent failure mode.

An advantage of requiring all data nodes to accept each value is that it requires less storage to achieve the same level of fault-tolerance. A primary-backup system that must tolerate f failures requires f+1 data nodes, whereas a naive implementation of the equivalent majority-based system would require 2f+1 data nodes. Cheap Paxos is an alternative approach that achieves f-failure resilience while requiring only f+1 main processors (i.e. primary-backup data nodes) and f auxiliary nodes (i.e. primary-backup master nodes). The disadvantage of Cheap Paxos is that it requires approximately equal numbers of main and auxiliary processors, whereas a primary-backup system can add data nodes for extra read capacity without having to add master nodes.

One advantage of requiring fewer than all B backup nodes to respond is that it may reduce the latency experienced by the client. For example, if data must be replicated by a mere majority of data nodes then the client latency is approximately the median latency between primary and backups, whereas if data must be replicated at all nodes then the client latency is at least the maximum such latency.

A second, related, advantage is that it may be quite common for nodes to experience temporary unavailability (e.g. due to a GC pause) and then recover, which can be handled without the full disruptive failover-and-reconfigure process if a response from the temporarily-unavailable node isn’t required for progress.

In cases where fewer than all B backups are needed, each phase-I quorum must contain more than one data node, so the failover process would require the active node to communicate with other data nodes in order to receive a phase-I quorum of offer-vote and promised messages, and this communication may also result in offer-catch-up messages and subsequent synchronisation between the data nodes.

There is a considerable amount of further generality to explore here too. To give a flavour of the possibilities, consider a WAN-like setup with a cluster split between one main region and three satellite regions as pictured below. One possible quorum structure is to normally require writes to be acknowledged at at least two data nodes in the main region as well as at least one satellite node.

As before, the other phase-II quorums are all majorities (i.e. pairs) of master nodes. The corresponding phase-I quorums are:

• any pair of master nodes together with any pair of data nodes in the main region, and

• any pair of master nodes together with all three satellite data nodes.

With this configuration the system is resilient to the loss of any one entire region, but does not require an unduly large amount of resources in the satellite regions.